ChatGPT 教会了我：

如何使用朴素贝叶斯定理构建垃圾邮件分类器？

我一直在努力提高我的机器学习技能，我刚发现了这个金矿！

不知从何处开始，这就是我沮丧地打出的内容：

我对机器学习的基础知识掌握不是很满意。你能在我请求时给我一小段讲解和练习吗，这样我就能学会了吗？

然后！一个月过去了，我从未如此自信过，因为我对机器学习的基础知识有了更深入的了解，不再只是采用试错方法选择正确的模型。

学习需要时间。但有时，弄清楚怎样学习和学什么甚至需要更长的时间。这是我试图为那些对机器学习基础概念感兴趣的人简化旅程的尝试。

那么让我们开始吧!

目标

我们将使用贝叶斯定理构建分类器，以确定给定信息是否为垃圾邮件，基于它包含的单词。

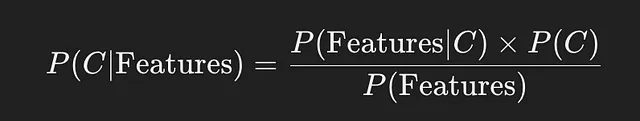
贝叶斯定理

让我们试着直观地理解这个问题。我们想要查找一个消息是否属于垃圾邮件类别或非垃圾邮件类别，给定消息的特征。上面的公式给出了概率，用来表明一个消息是否属于某个类别(垃圾或非垃圾)，给定消息的特征。这被称为后验概率。

后验可以使用上述公式计算，在此公式中，似然性乘以先验，然后除以特征的概率。

可能性是指我们可能已经具有的信息，即某个类别中存在某些特征的概率。例如，对于垃圾邮件类别，我们可以看到一条信息中包含“赢取、金钱、现在”等词语。因此，很可能许多垃圾邮件会包含类似赢取或金钱的词语。

以前的信息也是我们可以从数据集中获得的信息，即我们已经看到的所有信息，消息是垃圾邮件的可能性是多少。这为我们提供了在看到任何单词之前关于垃圾邮件的可能性的最初信念。

现在让我们试着从数据集中计算先验和似然。

训练数据集

这是我从ChatGPT获得的数据集。

dataset = [
    {"message": "win money now", "label": "spam"},
    {"message": "earn money from home", "label": "spam"},
    {"message": "meeting at work", "label": "not spam"},
    {"message": "urgent money transfer", "label": "spam"},
    {"message": "see you at the meeting", "label": "not spam"}

只看数据集，我们就可以看到5个消息中有3个是垃圾邮件。根据这个信息，我们可以假设以下关于先验概率的情况。

计算先验

我使用以下函数来计算并返回先验：

# Calculate Priors
def calculate_priors(dataset):
    """Calculates the prior probability of each class (spam or not spam)."""
    total_messages = len(dataset)
    spam_messages = sum(1 for data in dataset if data["label"] == "spam")

    not_spam_messages = total_messages - spam_messages
    return {
        "spam": spam_messages / total_messages,
        "not spam": not_spam_messages / total_messages
    }

对于我们的数据集，我们将获得以下先验概率：

垃圾邮件：0.6，非垃圾邮件：0.4

寻找可能性

下一步是找到可能性。让我们直觉地思考一下。可能性概率是指在给定类别（垃圾邮件或非垃圾邮件）的情况下，消息中存在某些特征的概率。那么，我们一直谈论的这些消息的特征是什么？对于这个问题，每个唯一的单词都是一个特征。为了获得这些特征的概率，我们需要首先对消息进行标记化处理，分割出这些特征，这意味着消息“赢钱现在”变成了["赢", "钱", "现在"]。这是我用于标记化的函数：

# Tokenize messages
def tokenize(message):
    """Simple tokenizer that splits message into words."""
    return message.lower().split()

要找到每个特征（即唯一单词）的可能性概率，我们首先需要为每个类别创建一个列表，其中包含属于相应类别的所有令牌化单词。

# Separating all words in messages belonging to spam or not_spam class to their r
# respective lists. 
allspam = []
allnotspam = []
for i in tokenized_messages:
    if(i[1]=="spam"):
        for j in i[0]:
            allspam.append(j)
    if(i[1]=="not spam"):
        for j in i[0]:
            allnotspam.append(j)

接下来，下面的函数接受列表（allspam和allnotspam）并计算垃圾邮件或非垃圾邮件列表中每个唯一单词的出现次数，并创建一个字典，其中唯一单词是键，它们的出现次数是值。为了找到在给定类别的消息中存在某个特征的可能性，即概率，我们只需将特征（或单词）的出现次数与每个allspam和allnotspam列表中的总单词数进行除法。

def createdict(wordarr):
    word_dict = {}
    for i in wordarr:
        if i in word_dict.keys():
            word_dict[i] += 1
        else:
            word_dict[i] = 1
    return word_dict

work_dict_spam = createdict(allspam)
work_dict_notspam = createdict(allnotspam)

# The likelihood P(Feature|Class=spam) for each word
prob_spam = {k: v / len(allspam) for k, v in work_dict_spam.items()}
# The likelihood P(Feature|Class=not_spam) for each word
prob_not_spam = {k:  v / len(allnotspam) for k, v in work_dict_notspam.items()}

计算后验概率

现在我们有先验概率和似然概率。我们可以找到后验概率！请注意，我在下面的公式中没有包括P(Features)。这是因为P(Features)不管是哪个类别（垃圾邮件或非垃圾邮件）都是相同的，所以加上它对我们来说并没有任何价值。

def posterior(x,prob,prior):
    if x in prob.keys():
        return prob[x]*prior 
    else :
        return 0.001

因此，对于我们想要检查是否为垃圾邮件的某个消息中的一个单词，我们首先查看该单词是否已经存在于词典（prob_spam或prob_not_spam）中，其中每个单词的概率已经计算出来。如果是，我们使用该概率来获取先验概率。如果该单词在该词典中不存在，我们为该单词分配一个非常小（接近零）的后验概率。我将在下面解释我们为什么这样做。

模型实施

以下代码根据训练数据集中计算的先验和似然来为每条信息提供模型的预测结果。我已经添加了注释来显示代码的工作原理。

def check(test,prob_spam,prob_not_spam):
    test_arr = tokenize(test) #turn the messages into tokens of words
    spam_ = []
    notspam = []
    for i in test_arr: 

# get posterior probability for each word given that the class is spam
# 0.6 is the prior for spam class
        spam_.append(posterior(i,prob_spam,0.6)) 

# get posterior probability for each word given that the class is not_spam
# 0.4 is the prior for not_spam class
        notspam.append(posterior(i,prob_not_spam,0.4)) 

# converting list to numpy to make it easy to perform calculations below. 
    spam_np = np.array(spam_)
    notspam_np = np.array(notspam)

# compare the sum of the log for the posterior for spam class with the 
# sum of the log for the posterior of the not_spam class. 

    if(np.sum(np.log(spam_np))>np.sum(np.log(notspam_np))):
        predicted = "spam"
        print("Spam: " + test)
    else:
        predicted = "not spam"
        print("Not spam: " + test)
    return predicted

通过比较我们消息中单词给定两个类别的概率的对数之和，如果某类别的概率更高，我们就将这个类别分配给消息。

为什么我们要把概率的对数相加？

为此，我们需要回到贝叶斯定理：

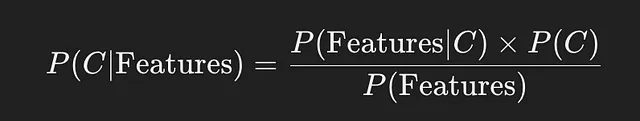
记住，每个特征都是我们信息中的一个单词。因此，我们正在尝试找出给定信息中所有这些单词的类别的联合概率。

朴素贝叶斯假设每个词是独立的，因此我们得到了如下分子的公式：

由于我们正在比较两个类别的后验概率，比较两个类别的对数不会改变我们的比较结果。取对数还可以避免很小的值相乘接近零时的数字不稳定性问题，当处理多个概率时这是一个常见问题。使用对数的性质 log(ab)=log(a)+log(b)，计算也变得简单得多，我们可以将其展开为：

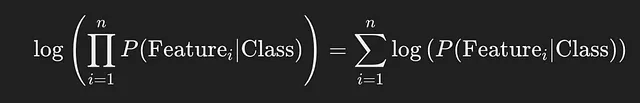
那么现在让我们谈谈为什么在我们预先计算的可能性中不存在的标记的后验概率中返回0.001，而不是返回0。这是因为log(0)是未定义的，并且分配一个非常小的数字（接近零）可以确保我们不会出现错误。如果你想深入了解，这个概念被称为拉普拉斯平滑。

测试和结果

下面是我自己创建的一个测试数据集，用来评估模型。

test_set = [
    {"message": "we have a meeting with John and Stuart", "label": "not spam"},
    {"message": "win a cash prize", "label": "spam"},
    {"message": "earn money fast", "label": "spam"},
    {"message": "see you at lunch", "label": "not spam"},
    {"message": "I have some very important information for you", "label": "not spam"}
]
accuracy = 0
for test in test_set:
    predicted = check(test['message'],prob_spam,prob_not_spam)
    if(predicted==test["label"]):
        accuracy+=1  
print("My models accuracy is {acc:.2f}".format(acc = accuracy/5*100))

Not spam: we have a meeting with John and Stuart
Spam: win a cash prize
Spam: earn money fast
Not spam: see you at lunch
Spam: I have some very important information for you
My models accuracy is 80.00

测试模型时，我能够获得80%的准确率！看到这样一个简单的模型能够学习不同单词与特定类别之间的关系，真的很酷。当然，这只是非常基础的。但我喜欢这种实现方式。你可以看到这些概念有多强大。

我想用一些观察来结束这篇文章，谈谈这个模型。