理解带主题建模的SVD
什么是奇异值分解(SVD)?奇异值分解是一种线性代数技术,用于将复杂/大矩阵分解或拆解为三个较简单的矩阵。
从本质上讲,它是一种数据简化或降维工具。比如说,如果您有非常高维度的数据,比如一个像素很多的图像,奇异值分解(SVD)会帮助我们将这些数据减少到用于分析或理解数据必要的关键特征。
想象一下,你有一组在2D或3D空间中的数据点,并且你想要理解它们的主要方向和强度。奇异值分解(SVD)可以帮助实现这个目标。
应用程序
1. 降维
- 用例:减少数据集中的特征数量,同时保留大部分信息。
- 在图像处理中,奇异值分解(SVD)可以通过仅保留最重要的奇异值和相应的奇异向量来压缩图像。这种方法称为低秩逼近,它显著减小了图像数据的大小,而又不会丢失太多质量。
2. 推荐系统
- 使用案例:建立系统向用户推荐物品(如电影、书籍、产品)。
- 示例:Netflix或Amazon的推荐引擎。SVD可以用来分解用户-物品评分矩阵,揭示代表潜在用户偏好和物品特征的潜在特性。然后可以利用这些特性来预测缺失的评分并向用户推荐物品。
3. 自然语言处理(NLP)
- 用例:识别文本数据中的模式,例如主题建模。
- 在一组文档的主题建模中,SVD可以分解术语-文档矩阵以识别潜在主题。每个主题是一组术语的组合,每个文档是这些主题的混合物,在对大量文本数据进行分类和总结时起到帮助作用。
4. 信号处理
- 用例:噪声降低和信号过滤。
- 在音频信号处理中,SVD可以用来将噪声与实际信号分离。通过分解信号矩阵并丢弃具有较低奇异值的部分(通常代表噪声),可以提高音频信号的质量。
5. 图像处理
- 用例: 特征提取和图像识别。
- 在面部识别系统中,奇异值分解(SVD)可以帮助提取面部图像中的关键特征。通过将图像数据分解为奇异值和向量,系统可以集中关注面部识别中最有信息量的特征。
对于任意 m x n矩阵 A,奇异值分解(SVD)找到3个矩阵 U,Σ和 V,使得 A = UΣV*。
U: m x m 正交矩阵。这可以被认为是您数据中的一组方向/特征。如果您的数据在某些方向上比其他方向更分散,或者具有关键特征,U 可以捕捉到这些。
Σ: m x n对角矩阵。该对角矩阵告诉您每个方向/特征的强度或重要性。较大的数字意味着更重要的方向。
V∗:n x n 正交矩阵。与 U 结合,这是另一组方向/特征,帮助我们理解原始数据的分布情况。
主题建模
让我们通过主题建模示例来理解它。
我们将使用一组小型虚构的句子来演示这一点。
示例语料库
让我们考虑以下四个句子的一个小语料库:
- 苹果和香蕉是水果。
- 水果如苹果和香蕉都是健康的。
- 汽车和自行车是交通工具。
- “像汽车和自行车这样的车辆需要燃料。”
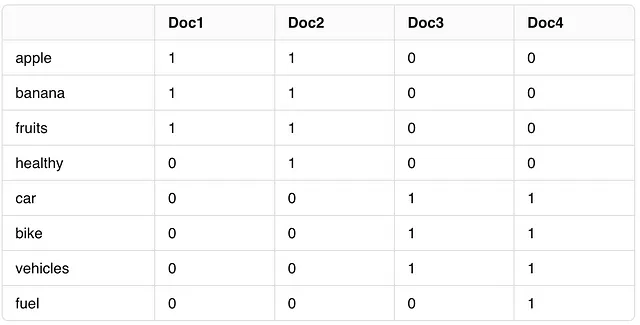
从这些句子中,我们将构建一个词-文档矩阵。为简单起见,我们将使用二进制频率来表示单词在文档(句子)中的存在(1)或不存在(0)。
步骤1:构建术语-文档矩阵
首先,我们要确定我们语料库中的唯一词汇:[“苹果”,“香蕉”,“水果”,“健康”,“汽车”,“自行车”,“交通工具”,“燃料”]。我们将删除诸如[“the”,“a”]这样的停用词。基于这些词汇和我们语料库句子的词项-文档矩阵将如下所示:
步骤2:让我们应用奇异值分解(SVD)并进行分解。
矩阵U(左奇异向量):
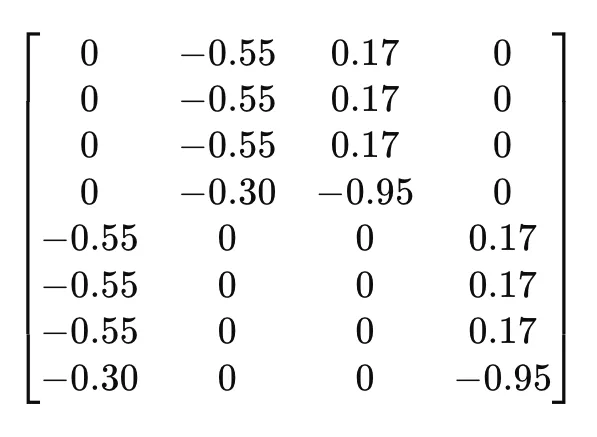
行:每一行对应于我们的词汇表中的一个单词。
栏目:这些栏目代表潜在的话题或概念。
简而言之,矩阵U展示了语料库中每个单词与每个已确认的潜在主题之间的关系。
解释具体的数值:
0 的值表示该单词与相应主题没有关联或相关性。例如,第一行中的第一个值为 0,意味着单词 "苹果" 与第一个潜在主题没有关联。
- 0.55的数值表明在数学空间中存在强烈的负相关性,但在主题建模中,我们通常关注的是绝对值。这表示与该行对应的单词(如“香蕉”或“水果”)与第二个潜在主题强烈相关。
潜在主题是如何确定的?在矩阵U中,每一列代表一个潜在主题。这些主题是抽象的,并且是从数据中的模式和关系推导出来的。SVD算法确定能够捕捉到数据中最大方差(信息)的维度(主题)。值得注意的是,该算法并不以人类的方式“决定”主题。它不会将它们标记为“水果”或“交通工具”。相反,它通过数学方式构建能够捕捉到术语-文档矩阵中最显著模式的维度。例如,如果在U的第一列中,某些词如“苹果”和“香蕉”有较高的值,并且这些词被认为是水果,那么你可以将这个潜在主题解释为与“水果”相关。
Σ矩阵(奇异值):
矩阵Σ在SVD中是一个对角矩阵,其中包含分解矩阵(在我们的情况下是词项-文档矩阵)的奇异值。以下是这些奇异值所代表的意义:
- 对角值: Σ的对角线上的值是奇异值。它们始终为非负数,并且通常按降序排列。在我们的示例中 :

2. 话题的重要性:每个奇异值对应着语料库中一种潜在话题的“强度”或“重要性”。较高的奇异值表示该话题能够更好地捕捉语料库中的方差(或信息)。
3. 降维:通过选择前k个奇异值(以及在U和V^T中对应的向量),我们可以近似原始矩阵。这在降低数据复杂度的同时保留最重要的方面非常有用。
矩阵 V^T(右奇异向量):
矩阵 V^T 是 SVD 中矩阵 V 的转置,由右奇异向量组成。这个矩阵与我们语料库中的文档相关。
- V^T 中的行:V^T 中的每一行对应于在 SVD 过程中识别出的潜在主题。
- V^T 中的列:每列代表原始语料库中的一个文档。
- V^T中的值:矩阵中的值表示每个文档中每个潜在主题的重要性。
在我们的例子中:
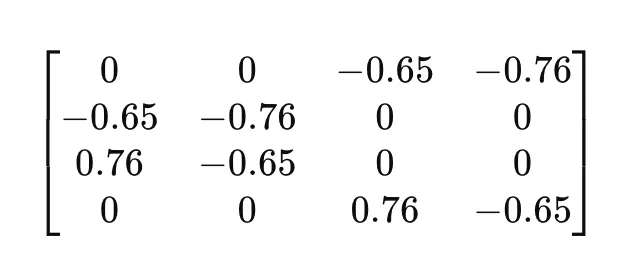
译文: 解释V^T:例如,V^T的第一行显示了第一个潜在主题在所有文档中的贡献。在特定列中的较高绝对值表示相应的主题在该文档中更为普遍。
何时使用SVD或PCA:
- 使用SVD(奇异值分解)的情况:
- 您正在处理稀疏数据。奇异值分解 (SVD) 可以高效地处理稀疏数据。
- 您的数据未居中,由于数据的性质或计算限制,您更倾向于不居中处理。
- 您正在处理需要奇异值和奇异向量的应用程序,例如潜在语义分析或复杂方程系统。
- 使用主成分分析(PCA)的情况包括:
- 您的主要目标是降维,以捕捉数据中的最大方差。
- 以原始特征的解释性为关键。
- 您正在处理大量数据,计算效率是首要考虑因素。