如何使用ChatGPT和Python赢得17.3亿美元的Powerball大奖

剧透警告:这将不起作用... 还是会起作用吗?🤔
本指南将向您展示如何使用真实的历史Powerball数据、一点人工智能以及一些Python编程来预测今晚Powerball抽奖的中奖号码(不用担心,所有代码都将由ChatGPT编写)。请跟随我直到最后,我将提供下一期中奖彩票号码。祝我好运!
过程
我会为您省略有关数据收集过程的细节,但数据集只是存储在一个CSV文件中的所有Powerball彩票抽奖的历史记录。这种类型的数据可以在几个州彩票网站以及其他资源中找到。
有了我们准备好的历史Powerball号码,我们只需要将文件输入ChatGPT并提供一些指导。然后,ChatGPT将为我们建立一个机器学习流程,我们可以使用它来预测获胜号码。轻而易举。
如果你想亲自尝试这个,请准备以下材料:
- ChatGPT Plus的主要特点是增强的API使用权限,使用户能够独立于OpenAI Playground使用ChatGPT。ChatGPT Plus的订阅费用为每月20美元,在将来可能会提供更多额外功能和优惠。作为ChatGPT Plus订阅者,您将享受到更快的模型响应时间和较低的队列等待时间。OpenAI非常重视用户的反馈,以不断改进和优化ChatGPT Plus的功能。
- 您选择的Python/代码编辑器
- 一个计算金钱的机器(用于你的赢利)
自定义说明
在侧边栏菜单中找到自定义指示。
启用新聊天并保存。
设置
开始新的聊天。
选择高级数据分析
为了简洁起见,我只提供了对话中的一些选定提示。希望这能激发出与ChatGPT进行不同互动以实现您自己目标的创意。接下来,我将提供ChatGPT为各种机器学习模型构建的代码。
对话
首先,我们提供文件和一些建议。
ChatGPT的回答以紫色方块标注。
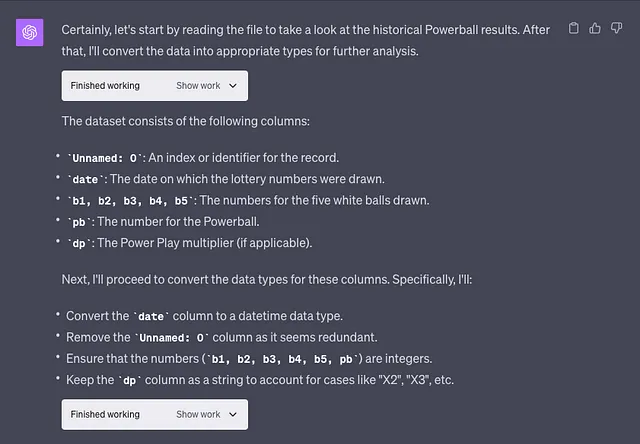
用户的提示以蓝色方块表示。请记住这一点。





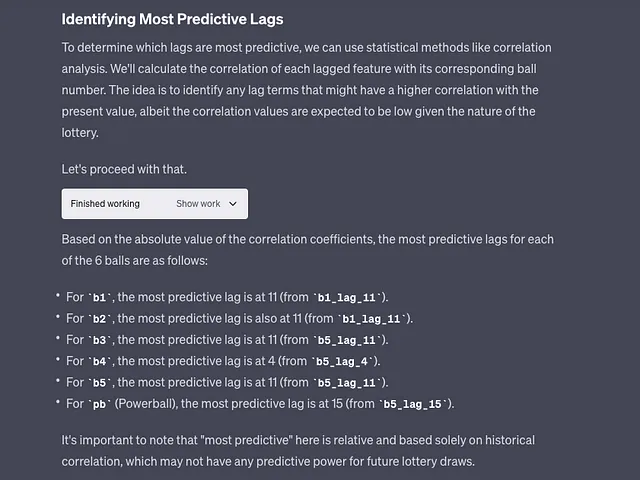


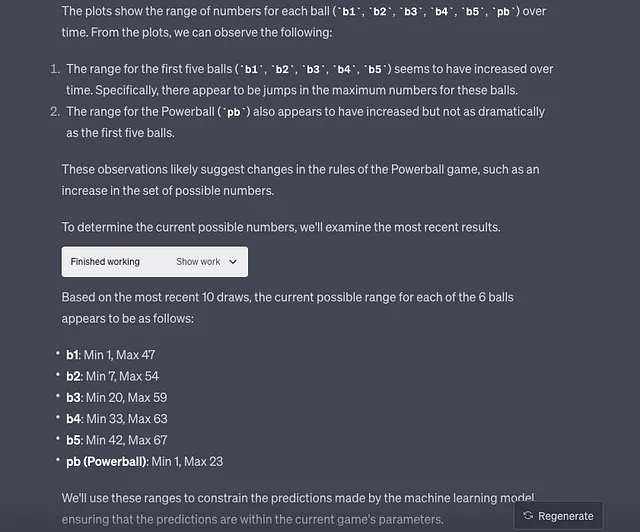

机器学习模型(由ChatGPT-4编写):
随机森林
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 1. Data Reading and Cleaning
df = pd.read_csv('historical_data.csv')
df.drop(columns=['Unnamed: 0', 'dp'], inplace=True)
df['date'] = pd.to_datetime(df['date'])
ball_cols = ['b1', 'b2', 'b3', 'b4', 'b5', 'pb']
df[ball_cols] = df[ball_cols].astype(int)
# 2. Feature Engineering - Lagged Variables
max_lag = 20 # Max number of lags to create for each ball
lagged_df = df.copy()
for col in ball_cols:
for lag in range(1, max_lag + 1):
lagged_df[f'{col}_lag_{lag}'] = lagged_df[col].shift(lag)
lagged_df.dropna(inplace=True)
# Select the most predictive lags based on our earlier analysis
selected_lags = ['b1_lag_11', 'b1_lag_11', 'b5_lag_11', 'b5_lag_4', 'b5_lag_11', 'b5_lag_15']
# 3. Model Training
X = lagged_df[selected_lags]
y = lagged_df[ball_cols]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Using Random Forest as the model
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 4. Model Evaluation
y_pred = model.predict(X_test)
test_score = mean_squared_error(y_test, y_pred, squared=False)
print(f"Test RMSE: {test_score}")
# 5. Prediction of Next Winning Numbers
next_X = lagged_df[selected_lags].iloc[-1].values.reshape(1, -1)
next_pred = model.predict(next_X)
next_pred = np.round(next_pred).astype(int)
# Ensure the predicted numbers are within the current game's parameters
next_pred = np.clip(next_pred, [1, 7, 20, 33, 42, 1], [47, 54, 59, 63, 67, 23])
print(f"Here are the next winning lottery numbers: b1={next_pred[0][0]}, b2={next_pred[0][1]}, b3={next_pred[0][2]}, b4={next_pred[0][3]}, b5={next_pred[0][4]}, pb={next_pred[0][5]}")自定义概率模型
import pandas as pd
import numpy as np
from collections import Counter
# 1. Data Reading and Cleaning
df = pd.read_csv('historical_data.csv')
df.drop(columns=['Unnamed: 0', 'dp'], inplace=True)
df['date'] = pd.to_datetime(df['date'])
ball_cols = ['b1', 'b2', 'b3', 'b4', 'b5', 'pb']
df[ball_cols] = df[ball_cols].astype(int)
# 2. Identify Current Range Based on Most Recent Draws
recent_results = df.nlargest(10, 'date')
current_range = {}
for col in ball_cols:
current_range[col] = {
'min': recent_results[col].min(),
'max': recent_results[col].max()
}
# 3. Custom Probabilistic Model
# Filter data to include only the most recent results (assuming current rules started from 2019 onwards)
recent_data = df[df['date'] >= '2019-01-01']
# Calculate the frequency distribution for each ball
frequency_distributions = {}
for col in ball_cols:
frequency_distributions[col] = Counter(recent_data[col])
# Normalize the frequencies to convert them into probabilities
probability_distributions = {}
for col, freq_dist in frequency_distributions.items():
total_count = sum(freq_dist.values())
probability_distributions[col] = {k: v / total_count for k, v in freq_dist.items()}
# Use Monte Carlo simulation to sample from this distribution to predict the next numbers
np.random.seed(42) # for reproducibility
def sample_next_number(prob_dist):
numbers = list(prob_dist.keys())
probabilities = list(prob_dist.values())
return np.random.choice(numbers, p=probabilities)
next_predicted_numbers = {}
for col in ball_cols:
next_predicted_numbers[col] = sample_next_number(probability_distributions[col])
# Ensure the numbers are within the current game's parameters
for col, val in next_predicted_numbers.items():
min_val, max_val = current_range[col]['min'], current_range[col]['max']
next_predicted_numbers[col] = min(max_val, max(min_val, val))
print(f"Here are the next winning lottery numbers: {next_predicted_numbers}")
贝叶斯推理模型
import pandas as pd
import numpy as np
from collections import Counter
from scipy.stats import beta
# 1. Data Reading and Cleaning
df = pd.read_csv('historical_data.csv')
df.drop(columns=['Unnamed: 0', 'dp'], inplace=True)
df['date'] = pd.to_datetime(df['date'])
ball_cols = ['b1', 'b2', 'b3', 'b4', 'b5', 'pb']
df[ball_cols] = df[ball_cols].astype(int)
# 2. Identify Current Range Based on Most Recent Draws
recent_results = df.nlargest(10, 'date')
current_range = {}
for col in ball_cols:
current_range[col] = {
'min': recent_results[col].min(),
'max': recent_results[col].max()
}
# 3. Bayesian Inference Model
# Filter data to include only the most recent results (assuming current rules started from 2019 onwards)
recent_data = df[df['date'] >= '2019-01-01']
# Step 1: Use a prior probability distribution based on historical frequency
frequency_distributions = {}
for col in ball_cols:
frequency_distributions[col] = Counter(recent_data[col])
# Step 2 & 3: Use Bayesian updating to generate a posterior distribution
# Here, we use a Beta distribution for simplicity
posterior_distributions = {}
for col in ball_cols:
alpha_prior = 1
beta_prior = 1
alpha_posterior = alpha_prior + sum(frequency_distributions[col].values())
beta_posterior = beta_prior + len(recent_data) - sum(frequency_distributions[col].values())
posterior_distributions[col] = beta(alpha_posterior, beta_posterior)
# Step 4: Sample the most probable numbers from the posterior distributions
np.random.seed(42) # for reproducibility
next_predicted_numbers = {}
for col in ball_cols:
next_predicted_numbers[col] = int(posterior_distributions[col].mean() * current_range[col]['max'])
# Ensure the numbers are within the current game's parameters
for col, val in next_predicted_numbers.items():
min_val, max_val = current_range[col]['min'], current_range[col]['max']
next_predicted_numbers[col] = min(max_val, max(min_val, val))
print(f"Here are the next winning lottery numbers: {next_predicted_numbers}")LSTM(长短期记忆)
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import LSTM, Dense
# 1. Data Reading and Cleaning
df = pd.read_csv('historical_data.csv')
df.drop(columns=['Unnamed: 0', 'dp'], inplace=True)
df['date'] = pd.to_datetime(df['date'])
ball_cols = ['b1', 'b2', 'b3', 'b4', 'b5', 'pb']
df[ball_cols] = df[ball_cols].astype(int)
# 2. Identify Current Range Based on Most Recent Draws
recent_results = df.nlargest(10, 'date')
current_range = {}
for col in ball_cols:
current_range[col] = {
'min': recent_results[col].min(),
'max': recent_results[col].max()
}
# 3. LSTM Model
# Step 1: Preprocess the data for LSTM
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(df[ball_cols])
X, y = [], []
for i in range(1, len(df)):
X.append(scaled_data[i-1:i])
y.append(scaled_data[i])
X, y = np.array(X), np.array(y)
# Step 2: Train LSTM model for each ball
next_predicted_numbers = {}
for idx, col in enumerate(ball_cols):
model = Sequential()
model.add(LSTM(50, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X, y[:, idx], epochs=50, verbose=0)
# Step 3: Predict the next number for each ball
next_num_scaled = model.predict(X[-1].reshape(1, 1, X.shape[2]))
next_num = scaler.inverse_transform(np.hstack([next_num_scaled if i == idx else np.zeros((1, 1)) for i in range(len(ball_cols))]))[0][idx]
next_predicted_numbers[col] = int(round(next_num))
# Step 4: Ensure the numbers are within the current game's parameters
for col, val in next_predicted_numbers.items():
min_val, max_val = current_range[col]['min'], current_range[col]['max']
next_predicted_numbers[col] = min(max_val, max(min_val, val))
print(f"Here are the next winning lottery numbers: {next_predicted_numbers}")集成学习
# Full code with feature engineering and ensemble learning
# Import required libraries
import pandas as pd
import numpy as np
from collections import Counter
from scipy.stats import beta
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import LSTM, Dense
# Function to sample next number based on calculated probabilities (for Monte Carlo)
def sample_next_number(prob_dist):
numbers = list(prob_dist.keys())
probabilities = list(prob_dist.values())
return np.random.choice(numbers, p=probabilities)
# Initialize DataFrame to store ensemble predictions
ensemble_predictions = pd.DataFrame()
# 1. Data Reading and Cleaning
df = pd.read_csv('historical_data.csv') # Replace with your file path
df.drop(columns=['Unnamed: 0', 'dp'], inplace=True)
df['date'] = pd.to_datetime(df['date'])
ball_cols = ['b1', 'b2', 'b3', 'b4', 'b5', 'pb']
df[ball_cols] = df[ball_cols].astype(int)
# 1.5 Feature Engineering: Create lag variables
lags = [1, 4, 11, 15]
for col in ball_cols:
for lag in lags:
df[f"{col}_lag_{lag}"] = df[col].shift(lag)
# Drop rows with NaN values generated due to lag
df.dropna(inplace=True)
# 2. Identify Current Range Based on Most Recent Draws
recent_results = df.nlargest(10, 'date')
current_range = {}
for col in ball_cols:
current_range[col] = {
'min': recent_results[col].min(),
'max': recent_results[col].max()
}
# 3. Random Forest Predictions
# (For demonstration, using limited data and model parameters)
selected_lags = ['b1_lag_11', 'b2_lag_11', 'b3_lag_11', 'b4_lag_11', 'b5_lag_11', 'pb_lag_11']
X = df[selected_lags][-10:]
y = df[ball_cols][-10:]
model_rf = RandomForestRegressor(n_estimators=10)
model_rf.fit(X, y)
rf_predictions = model_rf.predict(X.iloc[-1].values.reshape(1, -1))[0]
# 4. Monte Carlo Predictions
# Calculate the frequency distribution for each ball
frequency_distributions = Counter(df['b1'][-10:])
# Normalize the frequencies to convert them into probabilities
total_count = sum(frequency_distributions.values())
probability_distribution = {k: v / total_count for k, v in frequency_distributions.items()}
mc_predictions = np.array([sample_next_number(probability_distribution) for _ in range(6)])
# 5. Bayesian Inference Predictions
# Calculate the frequency distribution for each ball
frequency_distributions = Counter(df['b1'][-10:])
# Use Bayesian updating to generate a posterior distribution
alpha_prior = 1
beta_prior = 1
alpha_posterior = alpha_prior + sum(frequency_distributions.values())
beta_posterior = beta_prior + len(df[-10:]) - sum(frequency_distributions.values())
posterior_distribution = beta(alpha_posterior, beta_posterior)
bayesian_predictions = np.array([int(posterior_distribution.mean() * current_range['b1']['max']) for _ in range(6)])
# 6. LSTM Predictions
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(df[ball_cols][-10:])
X, y = [], []
for i in range(1, len(df[-10:])):
X.append(scaled_data[i-1:i])
y.append(scaled_data[i])
X, y = np.array(X), np.array(y)
model_lstm = Sequential()
model_lstm.add(LSTM(50, input_shape=(X.shape[1], X.shape[2])))
model_lstm.add(Dense(1))
model_lstm.compile(optimizer='adam', loss='mean_squared_error')
model_lstm.fit(X, y[:, 0], epochs=50, verbose=0)
next_num_scaled = model_lstm.predict(X[-1].reshape(1, 1, X.shape[2]))
next_num = scaler.inverse_transform(np.hstack([next_num_scaled] + [np.zeros((1, 1)) for _ in range(5)]))[0][0]
lstm_predictions = np.array([int(round(next_num)) for _ in range(6)])
# 7. Ensemble Learning: Combine Predictions
ensemble_predictions = pd.DataFrame({
'RandomForest': rf_predictions,
'MonteCarlo': mc_predictions,
'Bayesian': bayesian_predictions,
'LSTM': lstm_predictions
})
ensemble_predictions['Final'] = ensemble_predictions.mean(axis=1).astype(int)
# 8. Ensure the numbers are within the current game's parameters
for idx, col in enumerate(ball_cols):
min_val, max_val = current_range[col]['min'], current_range[col]['max']
ensemble_predictions.loc[idx, 'Final'] = min(max_val, max(min_val, ensemble_predictions.loc[idx, 'Final']))
ensemble_predictions['Final'].values异常检测
from sklearn.ensemble import IsolationForest
# Function to identify anomalies (lucky numbers) using Isolation Forest
def find_anomalies(data):
model = IsolationForest(contamination=0.1)
model.fit(data.reshape(-1, 1))
anomaly_pred = model.predict(data.reshape(-1, 1))
anomalies = data[anomaly_pred == -1]
return anomalies
# Initialize dictionary to store lucky numbers
lucky_numbers = {}
# Calculate the frequency distribution for each ball and find anomalies
for col in ball_cols:
frequency_distributions = df[col].value_counts().reset_index()
frequency_distributions.columns = ['Number', 'Frequency']
lucky_nums = find_anomalies(frequency_distributions['Frequency'].values)
lucky_numbers[col] = frequency_distributions[frequency_distributions['Frequency'].isin(lucky_nums)]['Number'].values
# Ensuring the lucky numbers are within the current game's parameters
for col in lucky_numbers.keys():
lucky_numbers[col] = np.clip(lucky_numbers[col], current_range[col]['min'], current_range[col]['max'])
print(f"Lucky numbers based on anomaly detection: {lucky_numbers}")用异常检测进行集成
# ... (Previous code for data loading, preprocessing, and ensemble prediction)
# Function to calculate weighted average of ensemble prediction and lucky numbers
def weighted_average(ensemble_pred, lucky_nums, ensemble_weight=0.7, lucky_weight=0.3):
if len(lucky_nums) == 0:
return ensemble_pred
return int(round(ensemble_weight * ensemble_pred + lucky_weight * np.mean(lucky_nums)))
# Calculate weighted average of ensemble prediction and lucky numbers
final_predictions = {}
for idx, col in enumerate(ball_cols):
final_predictions[col] = weighted_average(ensemble_predictions.loc[idx, 'Final'], lucky_numbers.get(col, []))
# Ensure the numbers are within the current game's parameters
for col, val in final_predictions.items():
min_val, max_val = current_range[col]['min'], current_range[col]['max']
final_predictions[col] = min(max_val, max(min_val, val))
print(f"Here are the next winning lottery numbers based on Ensemble Learning and Lucky Numbers: {final_predictions}")各位观众,这里有一组成功预测的中奖Powerball号码,它们是由使用ChatGPT生成的机器学习模型所产生的。
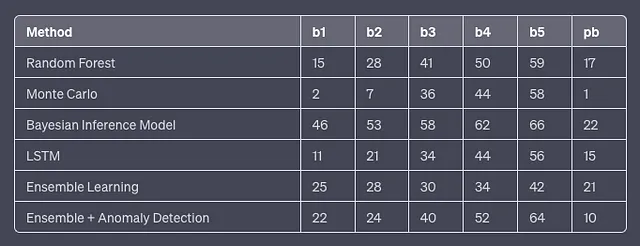
现在,我知道你在想什么。
但这里的意图实际上并不是赢得巨奖(虽然那会很好)。如果彩票是真正随机的,那么讨论的方法不会有助于预测结果。每次抽奖都是独立事件,其概率不受之前抽奖的影响。
这个练习旨在展示,曾经只有聪明才智的人才能接触到的一些非常先进的概念,现如今已突然变得在普通人中间也可以实现。基于大型语言模型(如ChatGPT)构建的生成型人工智能工具正在弥合非常聪明和普通个体之间的差距。那些努力有效利用这些新工具的人将对普通人拥有支配力。
选择权在你手中。








