LoRA: 从第一原则进行的低秩自适应
所有深度学习模型的核心都是由一系列矩阵乘法构成,其中穿插着Sigmoid、ReLU和GeLU等非线性函数的引入。近年来出现的大型语言模型(LLM)的增长已经证实了它们在各种应用中的异常潜力。然而,这些庞大的LLM的实际部署和微调对于数据科学团队来说存在着显著的成本和效率挑战。
这个领域的进步步伐惊人,不断有新的研究论文和软件包发布。这些资源旨在最大限度地减少使用LLMs进行培训和推测的成本和时间。考虑到这种快速进展,近期在我们的手持设备上运行LLMs也不足为奇。
在今天的讨论中,我将探讨一项关于低秩适应(LoRA)的突破性论文。这项研究提出了一种解决LLMs带来的成本和效率挑战的方法,即通过固定预训练模型权重并将可训练秩分解矩阵注入到Transformer架构的每一层中。这种创新性的方法显著减少了下游任务的可训练参数数量,从而大大降低了GPU内存要求,并提高了训练吞吐量。
通过利用线性代数的威力,LoRA为微调LLM提供了更可行的解决方案,无需额外的推理延迟或在模型质量上做出妥协。该论文甚至提供了LoRA有效性的实证证据,为更加简化的LLM调整方法铺平了道路。
我们将深入挖掘本文的细节,旨在阐明LoRA背后的基础概念,并理解其影响和潜在应用。我们的探究还将包括讨论新发布的工具和软件包,这些工具和软件包有助于将LoRA与PyTorch模型集成。这些资源为数据科学家在使用RoBERTa、DeBERTa和GPT-2模型等方面利用LoRA的优势提供了宝贵的支持。
加入我,让我们一起穿越复杂的大型语言模型,探索LoRA如何重新定义我们接近模型微调和部署的方式。
矩阵的秩是什么?
矩阵的秩是线性代数中的基本概念。它定义为矩阵中线性独立列(或等效,行)的最大数量。换句话说,它告诉我们矩阵表示的向量所涵盖的最大维数。粗略的定义可以是矩阵中所包含的信息量。
如果一个矩阵的秩等于其最小维数(行数或列数之一),则该矩阵被认为具有“满秩”。没有满秩的矩阵被称为秩缺陷。
以下是一个简单的例子:
考虑一个3x3的矩阵A:
A = [[1, 2, 3],
[2, 4, 6],
[3, 6, 9]]您可以看到,矩阵中的每一行都是其他行的倍数,因此它们都是线性相关的。在这种情况下,矩阵的秩为1,因为只有一行是线性无关的。
让我们再拿一个例子:
B = [[1, 2, 3],
[4, 0, 6],
[7, 8, 9]]在这个矩阵中,你可以看到没有任何一行是另一行的倍数,这意味着所有行都是线性独立的。因此,矩阵B的秩为3,因为有3个线性独立的行(或列)。
计算矩阵在Python中的秩,您可以使用numpy.linalg.matrix_rank()函数。例如:
import numpy as np
A = np.array([[1, 2, 3], [2, 4, 6], [3, 6, 9]])
print("Rank of A:", np.linalg.matrix_rank(A))
B = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("Rank of B:", np.linalg.matrix_rank(B))Rank of A: 1
Rank of B: 2此脚本将分别打印出“ A的秩为1”和“ B的秩为2”。请注意,在第二种情况下,即使没有行或列是其他行或列的精确倍数,矩阵仍然是秩不足的,因为其中一行可以表示为另外两行的线性组合。这证明了秩可以小于行数或列数。
矩阵的低秩近似
一对秩为r的矩阵A可以唯一地被分解为两个单独的矩阵。这可以表示为A = CR。在这里,C是一个m x r矩阵,其秩也是r。 C的列用作A的列空间的基础。另一方面,R是一个r x n矩阵,其秩也是r。R的行用作A的行空间的基础。
基本上,矩阵的秩是允许方程式 A(nxn) = C(nxr) R(rxn) 成立的最小值 r。需要注意的是,如果 r 小于矩阵的实际秩,仍然可以找到一个接近的解来满足方程式 A(nxn) = C(nxr) R(rxn)。
排名分解定理可以将矩阵 A 表示为两个矩阵的乘积,以可能更紧凑和数值稳定的方式捕捉 A 的基本结构。当 A 的排名很高但可以用低排名的矩阵很好地近似时,这个定理特别有用,这在应用中经常出现,例如图像处理和机器学习。
让我们用一个例子和Python代码来实践这个。
考虑一个5x5的矩阵A:
A = np.array([[19, 9, 12, 19, 8],
[ 0, 0, 0, 0, 0],
[ 3, 1, 0, 3, 0],
[ 6, 2, 0, 6, 0],
[25, 11, 12, 25, 8]])import numpy as np
A = np.array([[19, 9, 12, 19, 8],
[ 0, 0, 0, 0, 0],
[ 3, 1, 0, 3, 0],
[ 6, 2, 0, 6, 0],
[25, 11, 12, 25, 8]])
print("Rank of A:", np.linalg.matrix_rank(A))
Output:
Rank of A: 2让我们假设我们发现了一些满足A=CR的C(5x2)和R(2x5)。(可以使用SVD完成).
C = np.array([[4, 1],
[0, 0],
[0, 1],
[0, 2],
[4, 3]])
R = np.array([[4, 2, 3, 4, 2],
[3, 1, 0, 3, 0]])
print(" CR is :", C@R)
Output:
CR is : [ [19 9 12 19 8]
[ 0 0 0 0 0]
[ 3 1 0 3 0]
[ 6 2 0 6 0]
[25 11 12 25 8]]让我们先尝试做一个简单的线性模型(y = Wx + b)。
import torch
import numpy as np
torch.manual_seed(0)
# Dimensions
n, m = 10, 10 # n: input dimension, m: output dimension
#------------------------
# ignore this part of code I just made it make a rank deficient matrix
# it is highly probable that the W matrix will be a rank 2 through this process
nr,mr= 10, 2
W = torch.randn(nr,mr)@torch.randn(mr,nr)
# ----------------------
print("See how W looks like:\n",W)
b = torch.randn(n)
r= np.linalg.matrix_rank(W)
print("Rank of W:", r)
# Random input x
x = torch.randn(n)
# Compute y = Wx + b
y = W@ x + b
#--------------------------------
# this is just to exact rank factorization, it can be ignored sfely
# Perform SVD on W #
U, S, V = torch.svd(W)
# For rank-r factorization, keep only the first r singular values (and corresponding columns of U and V)
U_r = U[:, :r]
S_r = torch.diag(S[:r])
V_r = V[:, :r].t() # Transpose V_r to get the right dimensions
# Compute C = U_r * S_r and R = V_r
C = U_r@S_r
R = V_r
# -------------------------------------------
# Compute y' = CRx + b
y_prime = (C@R)@x+ b
print("Original y using W:\n", y)
print("y' computed using CR:\n", y_prime)
print("Total parameters of W:\n", W.shape[0]* W.shape[1])
print("Total parameters of C and R :\n", C.shape[0]* C.shape[1] + R.shape[0]* R.shape[1])Output:
See how W looks like:
tensor([[-1.0797, 0.5545, 0.8058, -0.7140, -0.1518, 1.0773, 2.3690, 0.8486,
-1.1825, -3.2632],
[-0.3303, 0.2283, 0.4145, -0.1924, -0.0215, 0.3276, 0.7926, 0.2233,
-0.3422, -0.9614],
[-0.5256, 0.9864, 2.4447, -0.0290, 0.2305, 0.5000, 1.9831, -0.0311,
-0.3369, -1.1376],
[ 0.7900, -1.1336, -2.6746, 0.1988, -0.1982, -0.7634, -2.5763, -0.1696,
0.6227, 1.9294],
[ 0.1258, 0.1458, 0.5090, 0.1768, 0.1071, -0.1327, -0.0323, -0.2294,
0.2079, 0.5128],
[ 0.7697, 0.0050, 0.5725, 0.6870, 0.2783, -0.7818, -1.2253, -0.8533,
0.9765, 2.5786],
[ 1.4157, -0.7814, -1.2121, 0.9120, 0.1760, -1.4108, -3.1692, -1.0791,
1.5325, 4.2447],
[-0.0119, 0.6050, 1.7245, 0.2584, 0.2528, -0.0086, 0.7198, -0.3620,
0.1865, 0.3410],
[ 1.0485, -0.6394, -1.0715, 0.6485, 0.1046, -1.0427, -2.4174, -0.7615,
1.1147, 3.1054],
[ 0.9088, 0.1936, 1.2136, 0.8946, 0.4084, -0.9295, -1.2294, -1.1239,
1.2155, 3.1628]])
Rank of W: 2
Original y using W:
tensor([ 1.6207, 2.1148, 2.3849, -2.3917, -1.2117, -4.9171, -3.9770, 0.5812,
-3.2889, -2.9090])
y' computed using CR:
tensor([ 1.6207, 2.1148, 2.3849, -2.3917, -1.2117, -4.9171, -3.9770, 0.5812,
-3.2889, -2.9090])
Total parameters of W:
100
Total parameters of C and R :
40这个例子清楚地证明了,我们可以使用两个不同的模型达到相同的结果:一个有100个参数,另一个只有40个。这是通过近似权重矩阵实现的。事实上,即使我们将“r”设置为小于权重矩阵的实际秩的值,我们仍然可以获得可接受的近似输出。
当训练模型像这样时,如果我们使用特定的训练样本和损失函数训练权重矩阵“W”,那么训练矩阵“C”和“R”将会更加容易和快速。同样的逻辑也适用于训练语言模型(LLM),以实现成本效益的训练。
LLM中的LORa
一些广泛的深度学习模型已经证明它们的权重矩阵通常存在于低秩空间内。值得注意的是,1000x1000维度的权重矩阵已经观察到存在于低至秩10的空间中。这导致了一共1⁰⁶个可训练参数。
为了清晰起见,让我们考虑训练语言模型(LLM)。假设我们有1000个维度的嵌入向量。这将产生1000x1000维的K、Q和V矩阵,每个矩阵产生1⁰⁶可训练参数。值得注意的是这些矩阵驻留在低秩空间内。如果这似乎复杂,只需记住LLM涉及一系列矩阵乘法,我们的目标是将这些矩阵压缩到较低的秩,以减少需要训练的参数数量。
在这个上下文中,微调过程被理解为模型内所有 W 到 W’ 矩阵的变换。我们选择保持 W 不变,以避免破坏基础模型的稳定性。相反,我们引入一个叫做 dW 的变化,并将其分解为两个低秩矩阵 A 和 B (dW = AB)。这显著减少了可训练参数的数量,从而使得这个过程更加高效。
W'(1000x1000) = W(1000x1000)+ dW(1000x1000)
dW(1000x1000) = A(1000x8) B(8x1000)
1000000 trainable params => 16000 trainable prameters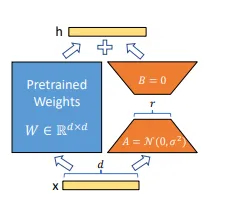
在实际应用中,我们不必训练语言模型(LLM)中的所有矩阵。只需训练少数目标模块并保持其余部分冻结,就能实现竞争性能。在低秩适应(LoRA)训练中,我们不是在寻找矩阵的确切秩,然后执行秩分解。相反,我们对预先假设的“r”值(超参数)得出近似解非常满意。
算法因此是直接的:
1. 冻结基础模型(W)。 2. 将W(dW)的变化近似为两个矩阵A和B的乘积,其中某些模块的‘r’是预先假定的。 3. 用基础模型训练适配器(A和B的乘积)。 4. 将训练好的适配器合并到基础模型中(W’= W + AB),然后进行推理。
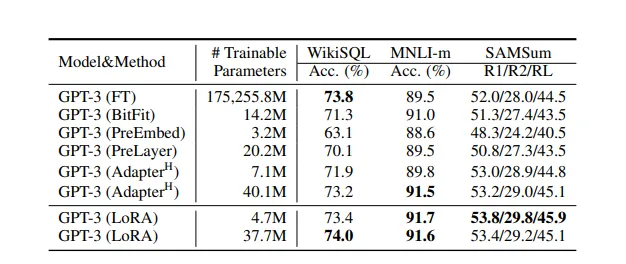
表演
根据该论文,我们在 LoRA 训练中并没有失去任何准确度,事实上,我们甚至获得了准确度,尽管我们将可训练参数的数量减少到原始数量的不到 1%。
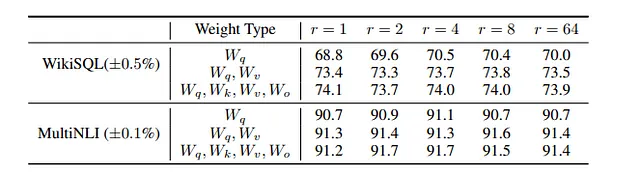
代码实现
代码只需使用peft库就能实现上述算法,如下所示的简单代码即可。完整代码可在此处访问。
from peft import PeftModel
from peft import LoraConfig, get_peft_model, prepare_model_for_int8_training, set_peft_model_state_dict
model = AutoModelForCausalLM.from_pretrained(
"bigcode/starcoder",
use_auth_token=True,
device_map={"": Accelerator().process_index},
)
# lora hyperparameters
lora_config = LoraConfig(r=8,target_modules = ["c_proj", "c_attn", "q_attn"])
model = get_peft_model(model, lora_config)
training_args = TrainingArguments(
...
)
trainer = Trainer(model=model, args=training_args,
train_dataset=train_data, eval_dataset=val_data)
print("Training...")
trainer.train()
# plugging the adapter into basemodel back
model = PeftModel.from_pretrained("bigcode/starcoder", peft_model_path)